![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
フーリエスペクトル解析 †(フーリエ)スペクトル解析は,ランダムデータから有用なシグナルを抽出するために,地震記録の分析においても頻繁に使われる基本的な解析手法である.通常の地震観測記録は,揺れの振幅の時間変化を記録するいわゆる時系列データであるが,地盤や建築構造物はある特定の周期(固有周期)の地震動を増幅させる特徴があることから,時系列波形データを周期ごとの振幅,すなわちスペクトルに分解することにより,地盤の増幅特性や構造物の応答特性を明らかにすることができる.また地盤や建物に対する入力としての地震動は,震源断層のせん断すべり運動によって発生し,地表に伝播したものであるが,こうした入力地震動に対するスペクトル解析によって,震源の破壊過程や伝播経路における減衰特性の解明が期待される. 1. フーリエスペクトル †1.1 フーリエ級数 †時間  このとき,右辺の級数をフーリエ級数またはフーリエ展開,その係数  なおここで用いられている関数 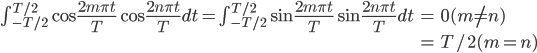 さらにm=nのときの積分値を1に正規化すると(この場合は係数 三角関数を指数関数に置き換えることにより,次のように複素フーリエ級数が導かれる. 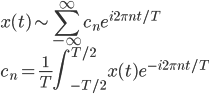 1.2 フーリエ積分 †複素フーリエ級数の周期区間を無限大とする極限を考えたとき,次の複素フーリエ積分が成り立つ.また,関数 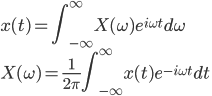 このとき, 2.3 フーリエ振幅スペクトルと位相スペクトル,および位相差分スペクトル †複素フーリエ係数 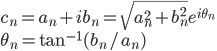 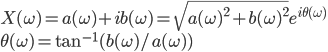 このときの絶対値 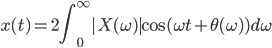 上式は,任意の時系列データ 位相スペクトルに対して,隣り合う周波数の位相角の差(位相差分)の頻度分布を位相差分スペクトルと呼ぶ.位相差分は負の値,すなわち0から 3 自己相関関数とパワースペクトル †時間の関数 ![C(\tau)=E[x(t)x(t+\tau)] C(\tau)=E[x(t)x(t+\tau)]](./teximg/09c6a2c2936f619451a1c8c6b3e41d0b3b05b2f18ce46f0ada0bd65ba15125c6.png) 定常確率過程の場合,上式は時間平均で置き換えられ,次のように時間ずれ 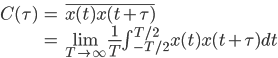 自己相関関数は偶関数( 一方,パワースペクトル密度関数 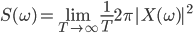 なお, 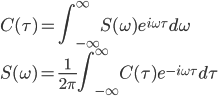 ここで, 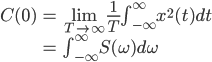 すなわち,パワースペクトル(密度) 4 相互相関関数とクロススペクトル,コヒーレンス †二つの時間変動の関数, 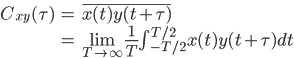 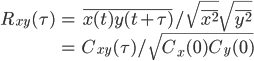 相互相関関数は,システムに対する入出力の関係(例えば入力地震動と建物の応答)や,ランダム変動場の空間相関などを推定する際によく用いられる. 相互相関関数のフーリエ変換として,クロススペクトル 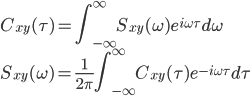 さらにクロススペクトル 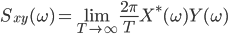 ここで*は共役関係を表す. クロススペクトルの二乗を二変数のパワースペクトルで正規化した量,またはその平方根をコヒーレンス 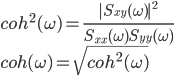 コヒーレンスは0から1の間で実数値をとる.またコヒーレンスは,入出力システムにおけるノイズの影響,システムのモデル化の誤差,システム特性自体の時間変動(非線形挙動)を反映する量として,主に解析精度の検証に用いられる. 5 フーリエスペクトル比と伝達関数 †地盤応答特性の推定や構造物の振動同定においては,対象となる地盤や構造物を地震動の応答システムとみなし,入力記録(基盤地震記録や建物基礎位置の記録)と出力記録(地表記録や上階の記録)からシステムの応答特性を推定する.このときの周波数領域における応答特性関数を一般に伝達関数と呼ぶ.いま,入力側の地震動 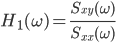 このようにして得られた伝達関数 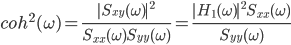 一方,地盤応答の伝達関数の推定では,入力となる地中地震波に表面波などの散逸成分が多く含まれていると考えられることから,以下に示すフーリエスペクトル比 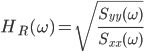 なお 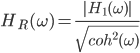 コヒーレンスは常に1以下の正の実数になるので, 6 FFTとスペクトルの平滑化 †ここまで,フーリエスペクトルとそれに関わるいくつかの概念を提示してきた.実際の観測記録は時間長が有限であり,また計算機処理の際には離散値を扱うので,
実地震データの解析から得られたフーリエ振幅スペクトルは振幅の凹凸が大きく,スペクトル比を取った場合などにはさらに凹凸の度合いが増幅する.こうした問題を避けるために,スペクトルの平滑化をおこなう.平滑化の操作は,周波数領域で一定のバンド幅をもつウィンドウ関数を乗じて移動平均を行うことでなされる.平滑化でよく用いられるウィンドウ関数としてはParzenウィンドウ,あるいはそのデジタル表記に相当するHanningウィンドウなどがある.Parzenウィンドウ 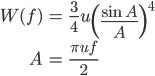 一方,Hanningウィンドウは中心周波数 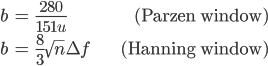 実際の平滑化では,バンド幅bを試行錯誤的に変化させながら,適切なスペクトルを求めていくこととなる. 参考文献 †
(田中、芝)
|